Replacing log2f with a Faster Approximation
2023-09-26
This problem came up while optimizing my implementation of WFC, but I figured it deserves its own post. One part of that algorithm is calculating Shannon entropies, which means calculating base-2 logarithms. And in this algorithm, a LOT of logarithms get calculated.
My program was very slow, so I profiled it and realized that most of the time was spent on C’s log2f function. This is generally a very well-implemented function that offers high precision and covers a lot of corner cases. It can, however, be a bit slow.
I did not need a too-precise logarithm function. I did need it to be much faster and I knew my inputs would always be positive numbers and never NaN, infinity, nor other special values. The solution was obvious - I would write my own log2f!
Now, one should not just start replacing functions from the standard library unless it really, provably is necessary. But in my case… well, I think it was necessary:
Approximating the binary logarithm
Library authors use a lot of tricks to implement floating-point math functions. In part they use math identities and approximation methods, in part they use bit-twiddling hacks on floating-point representations. Because of that the code can get quite involved and ends up looking very cryptic. Eg. here’s musl libc’s implementation of log2f: https://git.musl-libc.org/cgit/musl/tree/src/math/log2f.c, and of log2 (for doubles): https://git.musl-libc.org/cgit/musl/tree/src/math/log2.c. And this is an implementation of log (natural base) from a different codebase: https://www.netlib.org/fdlibm/e_log.c. As you can see, they are not simple. I am not qualified to explain those, so I will focus only on what I’ve implemented.
My first idea was to develop a Taylor polynomial, stick it in a function, and call it a day. All my inputs are in the range (0, 1], so the root would be 0.5 and I’d play around with different polynomial degrees for a good precision-speed tradeoff. There was one problem, though. Here’s what 5th-degree Taylor polynomial would look like:
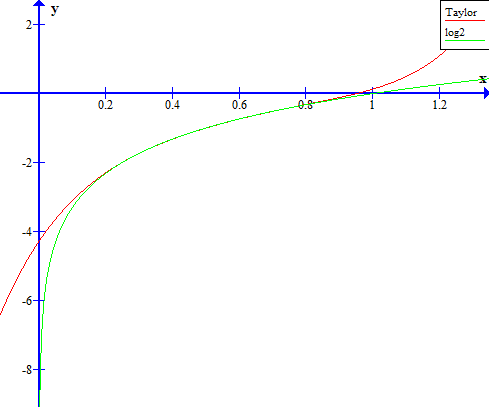
See how it diverges from the actual function as x nears zero? The y-axis is an asymptote for logarithms and no polynomial will simulate that well enough. This means that, for small enough numbers, the approximation error is inevitably going to be large. Thankfully, there is a solution - I’ll map my arguments to a different range. Floats are already represented as m * 2^e, where m is the mantissa and e is the exponent. This representation is convenient because it can easily be broken up by a binary logarithm:
log2(x) = log2(m * 2^e) = log2(m) + log2(2^e) = log2(m) + eFloat mantissa is always in the range [1, 2) and it turns out that approximating log2(x) in this range is quite easy. Hell, even log2(x) ~ x - 1 is not too far off, and x - 1 + 0.043 is even better.
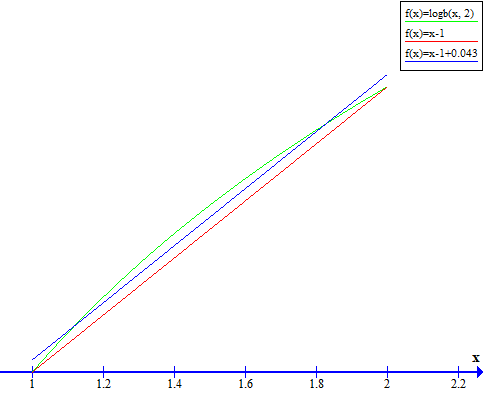
Taylor can now be applied on this range. But, in my research on how to approximate the binary logarithm, I learned that the Taylor approximation I was taught in school was not the best one. Two topics kept coming up - Chebyshev polynomials and the Remez algorithm.
To put it as simply as I can, Chebyshev polynomials (for a specified degree) aim to minimize the maximum error by constructing a polynomial whose error function will rise and fall in a sine-like fashion. Imagine the polynomial oscillating between above and below the function it approximates. For example, this is the error function of 5th-degree Chebyshev polynomial for log2(x) in the range [1, 2]:
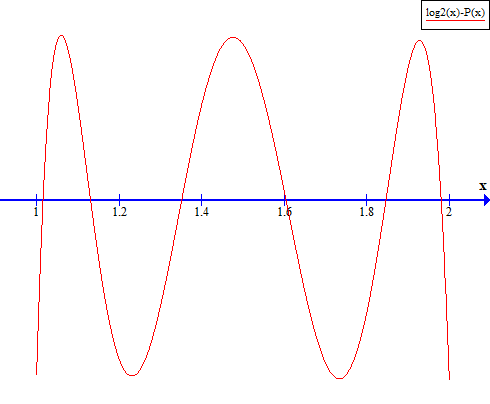
Remez algorithm computes the coefficients of Chebyshev polynomials. I won’t pretend to understand how it works, but fortunately, I don’t have to - I found a project called lolremez that runs the algorithm and outputs the coefficients. For the curious: check out reference links on the Remez algorithm at the bottom.
Implementation
Now that we have all that, what should the code look like?
First, it should extract the mantissa and exponent. This is done with some bit-twiddling. Here’s a refresher on the 32-bit float representation:
sign
| <--exponent---> <-----------------mantissa------------------>
V
31 30 23 22 0
. | . . . . . . . . | . . . . . . . . . . . . . . . . . . . . . . .The actual number is then: (-1)^sign * 2^(exponent - 127) * 1.{mantissa bits}.
Exponent can be extracted like this (assuming the number is positive):
int32_t xi;
memcpy(&xi, &x, sizeof(xi));
float e = (float)((xi >> 23) - 127);The second line reinterprets bytes of float as an integer to allow bitwise operations to be performed. memcpy is a standard-compliant way to reinterpret bytes of one type as a different type that works in both C and C++. That’s right, C and C++ rules are not the same. Compilers should optimize the call to memcpy away, so don’t worry about speed.
Mantissa can be extracted like this:
float m;
int32_t mxi = (xi & ((1 << 23) - 1)) | (127 << 23);
memcpy(&m, &mxi, sizeof(m));(1 << 23) - 1 is just a series of 23 ones at the lowest bits - this bitmask is used to select just the mantissa bits. The code then creates the bit representation for (-1)^0 * 2^(127 - 127) * 1.{mantissa bits}, which resolves to just the mantissa. It then reinterprets the bytes as a float.
Mantissa is always inside [1, 2), so the next step is to calculate the value of the Chebyshev polynomial. Eg. for the 3rd-degree case:
float l = 0.15824871f;
l = l * m + -1.051875f;
l = l * m + 3.0478842f;
l = l * m + -2.1536207f;The total logarithm value is then l + e.
You can find the final code for various degree approximations here.
Benchmark
Here is the benchmark code. My setup:
- Clang 16 with MSVC linker
- Windows 10
- Intel Core i7-8750H
The benchmark calls various implementations on one billion different values. In the tables below, err is the maximum absolute difference from the equivalent log2f result. time is the time in seconds it took to make a billion calls (plus some test overhead), averaged across 5 runs. err01 and time01 are the same, except calls were made on a different set of a billion values, all of which were in the range (0, 1].
I also added two functions I found at a GitHub repo called fastapprox. I have only a vague idea of how they’re computing the logarithm value (there’re a lot of magic constants), but they are reasonably fast and precise and therefore a nice reference for comparison.
These are the results after compiling with -O3 -march=native:
| function | time | err | time01 | err01 |
|---|---|---|---|---|
| log2f | 23.990800 |
0.000000 |
23.738200 |
0.000000 |
| fasterlog2 | 0.440600 |
0.057310 |
0.440400 |
0.057307 |
| fastlog2 | 0.453400 |
0.000153 |
0.440800 |
0.000147 |
| remez deg-1 | 0.441400 |
0.043037 |
0.441000 |
0.043036 |
| remez deg-2 | 0.442800 |
0.004940 |
0.442800 |
0.004940 |
| remez deg-3 | 0.443600 |
0.000639 |
0.441400 |
0.000639 |
| remez deg-4 | 0.451000 |
0.000090 |
0.440600 |
0.000090 |
| remez deg-5 | 0.445800 |
0.000015 |
0.440800 |
0.000015 |
These are the results after compiling with -O2 only (no -march):
| function | time | err | time01 | err01 |
|---|---|---|---|---|
| log2f | 23.943800 |
0.000000 |
23.718400 |
0.000000 |
| fasterlog2 | 0.439800 |
0.057310 |
0.442600 |
0.057307 |
| fastlog2 | 0.621800 |
0.000153 |
0.626800 |
0.000148 |
| remez deg-1 | 0.439800 |
0.043037 |
0.441600 |
0.043036 |
| remez deg-2 | 0.442600 |
0.004942 |
0.442400 |
0.004941 |
| remez deg-3 | 0.521800 |
0.000639 |
0.522400 |
0.000639 |
| remez deg-4 | 0.631000 |
0.000090 |
0.635600 |
0.000090 |
| remez deg-5 | 0.735400 |
0.000015 |
0.734400 |
0.000015 |
All of them are much faster than log2f. With -O3 -march=native times are so close that benchmark isn’t able to determine which functions are faster. With -O2 differences do show and it`s clear that adding more degrees makes for slower functions.
For the first four versions, precisions increased by about one decimal place with each degree added.
For my project, I ended up going with the 3rd-degree version. At lower degrees, my program’s outputs started to differ from when log2f was used. I figured that the 3rd-degree polynomial was a good compromise on precision and performance.
Conclusion
Don’t take this to mean you should replace all your calls to log2f - you probably shouldn’t. But if you ever run into a situation where a math function from the standard library is slow, hopefully this gives you some ideas on what you can do about it.
One thing I neglected to mention is that imprecisions on floating operations compound. If you use a slightly imprecise logarithm value in some calculations and then those results in additional calculations, results will diverge more and more from the correct one. What you use the logarithm value for is an important factor in deciding what loss of precision you can afford.
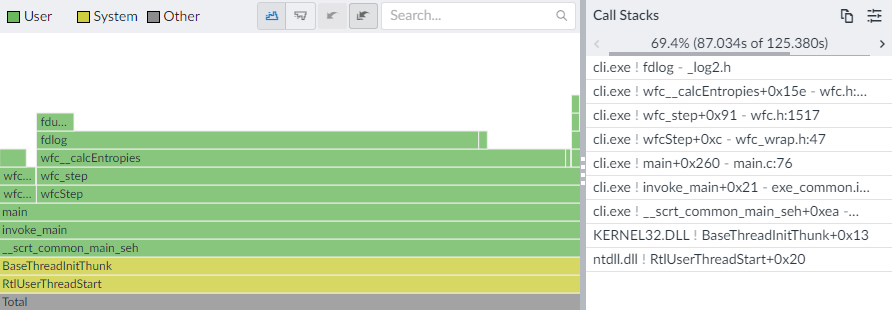
Anyway, as for my program from the start of the post, here’s what the profiler reported after I replaced log2f:
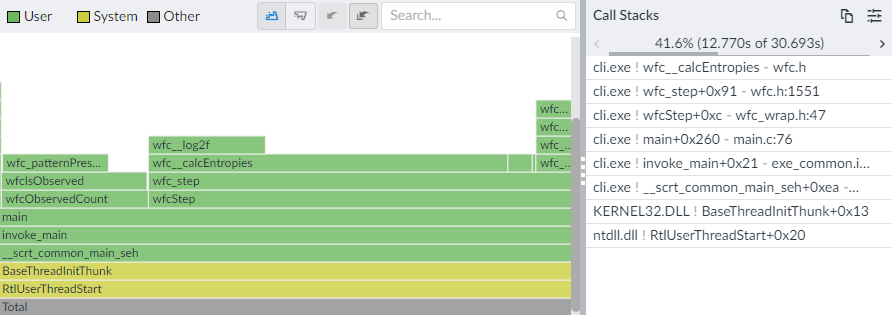
Those 125 seconds went down to 31 - nice!
References
https://austinhenley.com/blog/cosine.html
https://www.youtube.com/watch?v=p8u_k2LIZyo
https://en.wikipedia.org/wiki/Single-precision_floating-point_format
https://stackoverflow.com/questions/9411823/fast-log2float-x-implementation-c
https://github.com/romeric/fastapprox/blob/master/fastapprox/src/fastlog.h
https://www.flipcode.com/archives/Fast_log_Function.shtml
https://git.musl-libc.org/cgit/musl/tree/src/math/log2f.c
https://git.musl-libc.org/cgit/musl/tree/src/math/log2.c
https://www.netlib.org/fdlibm/e_log.c
http://jrfonseca.blogspot.com/2008/09/fast-sse2-pow-tables-or-polynomials.html
https://www1.icsi.berkeley.edu/pubs/techreports/TR-07-002.pdf
https://en.wikipedia.org/wiki/Chebyshev_polynomials
https://en.wikipedia.org/wiki/Remez_algorithm
https://www.boost.org/doc/libs/1_83_0/libs/math/doc/html/math_toolkit/remez.html
https://github.com/samhocevar/lolremez
https://github.com/samhocevar/lolremez/wiki/Implementation-details
https://stackoverflow.com/questions/38601780/can-memcpy-be-used-for-type-punning
https://gist.github.com/shafik/848ae25ee209f698763cffee272a58f8
https://cellperformance.beyond3d.com/articles/2006/06/understanding-strict-aliasing.html
https://www.vplesko.com/posts/wfc/devlog_0.html